Unsupervised Machine Learning: K-Means Clustering
Having discussed in detail supervised machine learning algorithms, we focus on an unsupervised machine learning algorithms: K-Means clustering.
Data Science can be an intimidating field, especially for beginners. There are so many terms thrown around and so much mathematics that it can overwhelm aspiring data scientists.
But our mantra is to apply the principle of KISS in whatever we do - Keep It Simple Stupid.
Here, we have compiled a list of the most commonly used machine learning and data science concepts and terms and tried to break it down into simple and easy-to-understand language without using any mathematical notation or technical jargon.
Our goal is to make data science accessible for everyone. So let’s get started and familiarize ourselves with the fundamentals of data science :)
It measures how many observations, both positive and negative, were correctly classified.
Accuracy = (TP + TN) / (TP + FP + TN + FN)
The Activation function is used to introduce non-linearity into the neural network helping it to learn more complex functions. Without this, the neural network would be only able to learn linear function which is a linear combination of its input data. An activation function is a function in an artificial neuron that delivers an output based on inputs.
It uses bootstrap sampling to obtain data subsets for training the base learners. The aim is to reduce the variance of a single classifier by averaging together multiple estimators e.g we train M different models on different subsets of the data(chosen randomly with replacement) and compute the ensemble.
For aggregating the outputs of base learners, bagging uses voting for classification and averaging for regression.
It refers to a family of algorithms that convert weak learners to strong learners.
The main principle of boosting is to fit a sequence of weak learners to weighted versions of the data. We take a sample from our data, build a model and then see how the model performed by looking at the correct and incorrect classifications. More weight is given to examples that were misclassified by earlier rounds i-e the weighting coefficients are increased for misclassified data and decreased for correctly classified data. The predictions are then combined through a weighted majority vote.
It is the difference between the average prediction of our model and the correct value.
The solid red line is the predictions of our model whereas the blue dots are the actual values.
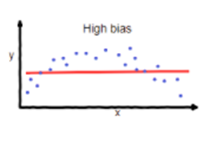
A model that has a very high bias oversimplifies the model which means the model is not able to make good predictions on either the training data or the test data. On the contrary, a model that has a very low bias complicates the model which means the model is able to make good predictions on the training data but fails to generalize well on the test data.
In machine learning, a good model is one that has a low bias and a low variance. However, both cannot be achieved at the same time.
Can a model be more complex and less complex at the same time? It doesn’t make sense, does it?
This is exactly the bias-variance trade-off. A more complex model means the model has high variance but low bias. A less complex model means the model has low variance but high bias.
Hence, we need to find the sweet spot between bias and variance when building our models so they can generalize well to data they have never seen before.
A method that involves drawing sample data repeatedly with replacement from a data source to estimate a population parameter.
Bootstrap sampling is used in ensemble learning called bagging to prevent over-fitting.
Categorical data are variables that contain label values rather than numeric values. They can be both nominal (in which order does not matter) such as gender (male, female) or ordinal (in which order does matter) such as education level(Bachelor, Master, Ph.D.)
There are two things you need to know about before you can understand the CLT: population and sample. In statistics, the population is the entire pool or group that we are interested in whereas a sample is a set of observations drawn from the population.
Let’s suppose we want to measure the weight of everyone in this world? All human beings present in the world make up the population. Now can we go and measure the weight of each and everyone across the globe? The answer is NO.
So what we do instead is that we take a sample from the population, measure the weights of all the people in the sample, and then make inferences about the weight of the population.
The CLT addresses exactly this question: what can we say about the average weight of all human beings in the world given a single sample?
The CLT states that if we sample from a population using a sufficiently large sample size, the mean of the samples will be normally distributed (assuming the sampling is done randomly). This will be true regardless of the distribution of the original population.
What constitutes a sufficiently large sample size? Most statisticians agree that N=30 and above is a reasonable size.
Therefore, with N=30, the mean of the sampling distribution will approximate the mean of the true population distribution.
Clustering problems involve data being divided into subsets. These subsets, also called clusters, contain data that are similar to each other. Different clusters reveal different details about the objects.
A confusion matrix is a table that is often used to describe the performance of a classification model (or "classifier") on a set of test data for which the true values are known.
Here are some terms associated with a confusion matrix:
True Positives: the model predicted positive and the actual outcome was also positive
False Positives: the model predicted positive but the actual outcome was not positive
True Negative: the model predicted negative and the actual outcome was also negative
False Negatives: the model predicted negative and the actual outcome was also negative
Whenever we are interested in estimating a population parameter, we take different samples of sufficiently large size and make inferences about the population based on our samples.
However, different samples from the same population will give different results. Hence, we can never specify an exact value for the parameter. We always specify a range within which our population parameter lies. A confidence interval, therefore, refers to the probability that a population parameter will fall between a set of values for a certain proportion of times.
It is used to deal with the uncertainty that results due to sampling error.
It measures the association between two variables. Two variables can be positively correlated, negatively correlated or have zero correlation.
If two variables have a positive correlation, an increase in one results in an increase in the other.
If two variables have a negative correlation, an increase in one results in a decrease in the other. If two variables have a zero correlation, an increase in one results in no change in the other.
A function that measures the performance of a Machine Learning model for given data by quantifying the error between predicted output and the ground truth. The objective of an ML model, therefore, is to find parameters that minimize the cost function.
It has multiple other names such as loss function, objective function, scoring function, or error function.
Instead of dividing the data into training and test sets, the training set is split into complementary subsets (also called folds), and in each iteration, the model is trained against a different combination of these subsets and validated against the remaining folds.
The following example illustrates a 5-fold cross-validation meaning the entire data set is divided into 5 subsets. In each iteration from 1 to 5, the model gets trained on 4 of the folds and gets tested on the remaining one.
The advantage is that the model gets trained and tested on every data instance as opposed to the train-test-split method where the model never gets to train on the test data, hence losing out on data the model could have seen and learned from to make better predictions.
A technique for synthesizing new data by modifying existing data in such a way that the target is not changed, or it is changed in a known way. Some ways to augment data include resizing, re-scaling, flipping, rotating, and adding noise.
A decision tree is a supervised machine learning algorithm mainly used for Regression and Classification. It breaks down a data set into smaller and smaller subsets while at the same time an associated decision tree is incrementally developed. The final result is a tree with decision nodes and leaf nodes. A decision tree can handle both categorical and numerical data.
A decision boundary or a decision surface is a hypersurface that divides the underlying feature space into two subspaces, one for each class. If the decision boundary is a hyperplane, then the classes are linearly separable.
The goal is to simplify the data by bringing it down from a higher dimension to a lower dimension without losing too much information to accelerate the training process and aid data visualization. The two main approaches to reducing dimensionality are Projection and Manifold Learning. The main technique used in machine learning to deal with the curse of dimensionality is Principal Component Analysis (PCA)
Expectation-Maximization (EM) is a method to estimate parameters for latent variables, whereby some variables can be observed directly, whereas others are latent and cannot be observed directly.
This technique combines several machine learning techniques into one predictive model to decrease variance(bagging) and bias(boosting) to improve predictions. It has two types:
Sequential Ensemble Methods where learners are generated sequentially. It exploits the dependence between the base learners. The overall performance is boosted by weighing previously misclassified examples
Parallel Ensemble Methods where the base learners are generated in parallel. It exploits the independence between the base learners since the total error can be reduced dramatically by averaging.
For Ensemble Methods to be accurate, the base learners have to be as accurate and diverse as possible.
It happens when the model predicts something as positive when it is not positive.
FPR= FP / (FP + TN)
It happens when the model does not predict something as positive when it is positive.
FNR= FN / (TP + FN)
The process of transforming raw data into features that better represent the underlying problem to the predictive models, resulting in improved model accuracy.
For example, combining multiple features that are highly correlated with each other and forming a new feature that results in better performance is an example of feature engineering. By doing so, we reduce the feature space and accelerate the training process.
A term used in machine learning to refer to all the features present in a data set. So if you have a data set with n features (this does not include the target variable), your feature space consists of n dimensions.
Feature scaling involves re-scaling the features such that they have the properties of a standard normal distribution with a mean of zero and a standard deviation of one.
As a rule of thumb, if you are using a machine learning algorithm that calculates the distance to find similarities between observations, it’s always a good idea to scale your features.
Gradient descent is an iterative optimization algorithm used in machine learning to minimize a loss function. It is used to find the best set of parameters by minimizing errors between predicted output and the ground truth.
Machine learning models have some hyperparameters that are set in advance and do not depend on the model e.g. the k in k-Nearest Neighbors is a hyperparameter that the user has to set. Similarly, there are some parameters that are learned by the model as it gets trained e.g the beta coefficients in linear regression or the support vectors in SVM.
Grid-search is a technique used to find the optimal hyperparameters of a model which results in the most ‘accurate’ predictions.
A Gaussian Mixture Model (GMM) is a model whereby for any given data point x, we assume that it comes from one of the k clusters, each with a particular Gaussian Distribution.
A hyperparameter is a parameter of a learning algorithm (not of the model). As such, it is not affected by the learning algorithm itself; it must be set prior to training and remains constant during training.
A subspace of a vector space that has a dimension one less than the dimension of the vector space. If we have a feature space of n dimensions i-e n features (excluding the target variable), the hyperplane would have (n-1) dimensions.
An unsupervised machine learning algorithm, K-means clustering partitions data into k clusters and starts by choosing centroids of each of the k clusters arbitrarily. Iteratively, it updates partitions by assigning points to the closest cluster, updating centroids, and repeating until convergence.
A supervised machine learning algorithm, KNN calculates the distance of a new data point to all other training data points. It then selects the K-nearest data points, where K is a hyperparameter and can be any integer but usually an odd value if the number of classes is two. Finally, it assigns the data point to the class to which the majority of the K data points belong.
Choosing a small value of K means the noise will have a higher influence on the result. On the contrary, a large value of K makes it computationally expensive.
A kernel is a way of computing the dot product of two vectors in some (possibly very high dimensional) feature space, which is why kernel functions are sometimes called “generalized dot product”
The kernel trick is a method of using a linear classifier to solve a nonlinear problem by transforming linearly inseparable data to linearly separable ones in a higher dimension.
A technique used to approximate the (linear) relationship between a continuous response variable and a set of predictor variables. Linear regression assumes a linear relationship between the predictor and the response variables.
A technique to predict the binary outcome from a linear combination of predictor variables when the response variable is categorical. It makes use of the sigmoid function which takes in a value and outputs a value between 0 and 1. Hence, the upper limit is 1 and the lower limit is 0 and we get a resulting S-shaped curve.
In logistic regression, we use the concept of the threshold value, which defines the probability of either 0 or 1. Such as values above the threshold value tend to 1, and a value below the threshold value tends to 0. Normally, the threshold is set at 0.5.
(Feeling Overwhelmed? We have built an all-in-one platform that takes care of the entire data science lifecycle. From importing a dataset to cleaning and preprocessing it, from building models to visualizing the results and finally deploying it, you won’t have to write even a SINGLE line of code. The goal is to make machine learning and data science accessible to everyone!)
It involves maximizing a likelihood function in order to find the probability distribution and parameters that best explain the observed data. The parameter values are found such that they maximize the likelihood that the process described by the model produced the data that was actually observed.
The statistical mean adds up all numbers in a data set and then divides the total by the number of data points. It is also called the expected value.
The most frequently occurring value in a dataset.
Median is a statistical measure that determines the middle value of a dataset listed in ascending order (i.e. from smallest to largest value)
Neural networks are a specific set of algorithms that are inspired by biological neural networks. They can adapt to the changing input, so the network generates the best possible result without needing to redesign the output criteria. They consist of inputs that get processed with weighted sums and Bias, with the help of Activation Functions, a hidden layer, and an output layer.
Image Source: A standard normal distribution that has mean 0 and std 1
If the data is distributed in such a manner that most values lie close to the mean value and the further you get from the mean, the data tends to decrease in a symmetrical fashion on both sides of the mean, then we say the data is normally distributed.
The following are the properties of Normal Distribution:
Machines are only able to understand numeric data but what if a variable is categorical?
There should be a way to convert categorical features into numerical features. Fortunately, there is.
One hot encoding is a technique to convert categorical variables into numeric variables.
The model is very good at predicting/ classifying on training data but fails to generalize well on test data. An overfit model has high variance and low bias.
To prevent a model from overfitting, add more data to training, reduce the complexity of the model, augment the data and increase dropouts.
An outlier is a value that lies outside the normal range of values of a given variable. They do not ‘fit’ or ‘gel in’ as they are distinct from the other data points and they do not fall into a common trend or pattern.
This is a very tricky concept so I’ll try to give an example to explain this intricate concept.
P-value is defined as the probability that we get a sample result by chance if there is NO effect in the population.
Didn’t get it? Let’s go through a quick example.
In statistics, we are often interested in comparing a null hypothesis that represents the status quo and an alternative hypothesis. Let’s suppose, we are interested in studying if a new drug is effective in curing a certain disease. Our null hypothesis is that the drug is not effective. Hence, the alternative hypothesis is that the drug is effective. To test our hypothesis, we form two groups: one to which no drug is given and the other to which a drug is administered.
Now, there can be two possible outcomes:
If we encounter the second outcome, we would be interested to know if the difference arose due to chance or is it statistically significant meaning the drug is indeed effective in curing the disease.
The p-value will tell us exactly this. If our p-value is lower than our significance level, we reject the null hypothesis
It measures how many observations predicted as positive are in fact positive.
Precision= True Positive / True Positive + False Positive
A curve that combines precision and recall in a single visualization. There is a tradeoff between precision and recall so the higher the precision, the lower the recall. As a rule of thumb, the higher on the y-axis your PR curve is, the better will be your model performance.
Knowing at which recall your precision starts to fall fast can help choose the threshold and deliver a better model.
A dimensionality reduction technique to obtain important variables in the form of components from a large set of variables available in a data set.
For example, you have a dataset with hundreds of features. Dealing with higher dimensional data can be painful and it’s always a good idea to be able to bring it down to lower dimensions and only be able to work with the features that contribute the most towards model performance.
A principal component is defined as a normalized linear combination of the original predictors in a dataset. For example, the first principal component is a linear combination of original predictor variables which captures the maximum variance in the dataset. It determines the direction of the highest variability in the data.
The first PC will have the highest variance, then the second PC, then the third, and so on.
All Principal Components are uncorrelated/ orthogonal to each other.
This often confuses many people but the principal components themselves are not features themselves. By looking at a principal component, we cannot determine which feature contributes towards the maximum variance.
Interpretation of the principal components has to be done by you.
The variable that is used to predict the target variable. It is also known as the input variable or the independent variable.
A probability density function (PDF) describes the probability of the value of a continuous random variable falling within a range. If the random variable can only have specific values (like throwing dice), a probability mass function (PMF) would be used to describe the probabilities of the outcomes.
A technique in machine learning that reduces the size of decision trees. It reduces the complexity of the final classifier, and hence improves predictive accuracy by the reduction of overfitting. Pruning can occur in:
A random quantity whose values depend on outcomes of a random phenomenon and that has an associated probability distribution.
When studying random variables, you will come across the example of rolling a die or flipping a coin.
Rolling a dice is a random event. Whenever we roll a die, the outcome can be a number from 1 to 6. The event of rolling a die is random but we can associate the outcome with a quantifiable number.
Let’s suppose you roll a die ten times. X can be a random variable describing the number of times the die turns out to be six. Or it can be the number of times it yields an odd number i-e the value is either a 1,3 or 5.
Random variables are often studied in the context of the probability of a random event. What is the probability of rolling a dice and obtaining a six? It’s 1/6.
One of the best ways to prevent a model from over-fitting is to reduce the number of features.
Regularization can do that for you. These are techniques meant to prevent a model from over-fitting by putting a constraint on the estimated coefficients to reduce the variance and decrease out of sample error. A penalty term is introduced to induce smoothness which prevents the model from over-fitting.
In a regularized regression model, we are minimizing the Sum of Squared Errors (SSE) plus a penalty term P. This penalty parameter constrains the size of the coefficients such that the only way the coefficients can increase is if we experience a comparable decrease in the sum of squared errors (SSE).
There are three common penalty parameters we can implement:
A chart that visualizes the tradeoff between True Positive Rate (TPR) and False Positive Rate (FPR). As a rule of thumb, the higher the TPR and the lower the FPR, the better your model will be. Curves that are on the top left side are better.
This metric is used when you care equally about the positive and negative classes. It tells the probability that a randomly chosen positive instance is ranked higher than a randomly chosen negative instance. It does this by calculating the area under the ROC curve.
It measures how many observations out of all the positive observations are classified as positive.
Recall= True Positive / (True positive + False Negative)
In statistics, we are interested in estimating the parameters of a population e.g the average weight of all humans in the world. From a practical perspective, that is not possible so we take a subset of humans, calculate their weights, and then make an inference about the average weight of all humans.
The subset of humans that we select for our analysis is our sample.
Sampling could be defined as a technique used to select and analyze a representative subset of data points to make inferences about the population.
Also called sampling bias, it occurs when the sample data that is gathered and prepared for modeling has characteristics that are not representative of the true, future population of cases the model will see.
For example, we are interested to know the average weight of humans in the world. We take a sample that only comprises children and excludes adults and old people. Hence, our sample is not a true representation of our population.
The standard deviation is a statistic that measures the dispersion of a dataset relative to its mean and is calculated as the square root of the variance. If the data points are further from the mean, there is a higher deviation within the data set; thus, the more spread out the data, the higher the standard deviation.
In Supervised machine learning, we train the model using a labeled data set. While training, we have to explicitly provide the correct labels and the algorithm tries to learn the pattern from input to output.
Basically, we are telling the machine that when the input is x1 the output is y1, when the input is x2 the output is y2, and so on.
The most common Supervised Machine Learning Algorithms are: Support Vector Machines, Regression, Naive Bayes, Decision Trees, K-nearest Neighbor Algorithm, and Neural Networks.
Supervised learning uses data that is completely labeled, whereas unsupervised learning uses no training data. In the case of semi-supervised learning, the training data contains a small amount of labeled data and a large amount of unlabeled data.
A supervised machine learning algorithm, SVM checks for that hyperplane that is able to distinguish between the two classes. There can be many hyperplanes that can do this task but the objective is to find the hyperplane that has the highest margin which means maximum distances between the two classes.
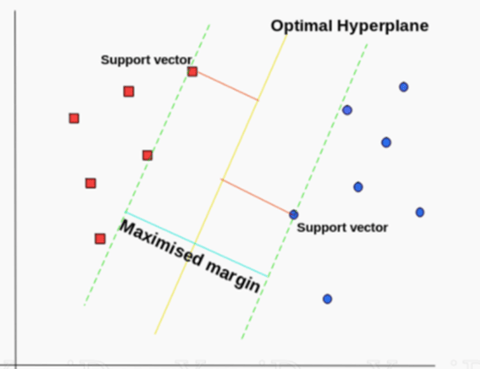
If the data is not linearly separable, then we use what’s called a kernel trick to make the data linearly separable by projecting it into a higher-dimensional space via some non-linear transformation.
As the name suggests, it is the variable that is predicted by the response variables. There can be only one target variable. It is also known as the dependent variable, the output variable, or the response variable.
The model is not even able to predict data well on the training data. An under-fit model has high bias and low variance.
To prevent a model from under-fitting, increase the complexity of the model, add more features to the training set and reduce dropout.
In Unsupervised machine learning, the data set is not labeled. The algorithm needs to detect trends and patterns on its own since it is not provided with any pre-existing labels.
The most common Unsupervised Machine Learning Algorithms are: Clustering, Anomaly Detection, and Latent Variable Models
It reflects the variability of our model predictions for a given data point.
Let’s suppose we train our model on a given data set and get our predictions. Now, what happens if we input a new dataset in our model that it has never seen before? How much will the prediction values change?
We want our model to make good predictions on any data that it sees and not just memorize the data points on which it was trained. A model with high variance means the model has memorized what’s in the training data but does not generalize well on test data.
Let me give you a real-life example that will illustrate my point better.
As a student, when preparing for exams, we practice different kinds of problems to improve our understanding. The questions that we see and prepare before the exam is the training data and the questions that we see on the actual exam are the test data. A good student is the one who performs well on both the training data as well as the test data which in our case are the actual exam questions.
A student that does well on the training data but cannot perform well on the actual exam questions is said to have a high variance.
We hope this guide will give you a holistic understanding of the data science realm. It’s just the tip of the iceberg but mastering the basics will help you get started in your journey as a data scientist.
Want to start exploring some of these terms more? Trial The AI & Analytics Engine, you can get started with publicly available data sets and see data science in action.
Having discussed in detail supervised machine learning algorithms, we focus on an unsupervised machine learning algorithms: K-Means clustering.
This article answers questions on machine learning, through the 3 ML types: supervised learning, unsupervised learning, and reinforcement learning.
Clustering is an unsupervised machine learning method, where datapoints are organized into groups, or clusters, consisting of similar datapoints.